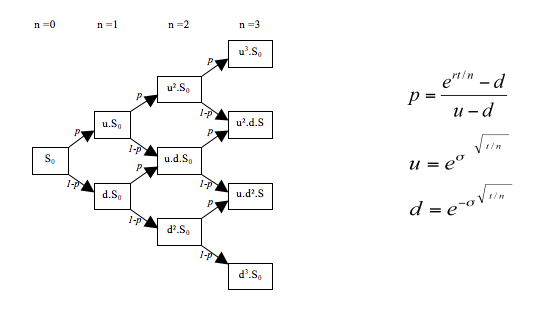
Le modèle Black-Scholes ou modèle Black-Scholes-Merton qui est un modèle mathématique du marché pour une action, dans lequel le prix de l’action est un processus stochastique en temps continu ; par opposition au modèle Cox Ross-Rubinstein (présenté ici) qui suit un processus stochastique en temps discret.

Ce modèle repose sur les hypothèses suivantes :
- Il n’y a pas d’opportunités d’arbitrage ;
- Le temps est une fonction continue ;
- Il est possible d’effectuer des ventes à découvert ;
- Il n’y a pas de coûts de transactions ;
- Il existe un taux d’intérêt sans risque, connu à l’avance et constant ;
- Tous les sous-jacents sont parfaitement divisibles (on peut par exemple acheter 1/100e d’action) ;
- Dans le cas d’une action, celle-ci ne paie pas de dividendes* entre le moment de l’évaluation de l’option et l’échéance de celle-ci.
Après avoir implémenté le modèle CRR, il était pour moi impossible de ne pas faire de même pour le modèle de Black-Scholes-Merton !
* Une extension du modèle permet de prendre en compte les dividendes, elle a été implémenté également.