Catégorie : Informatique

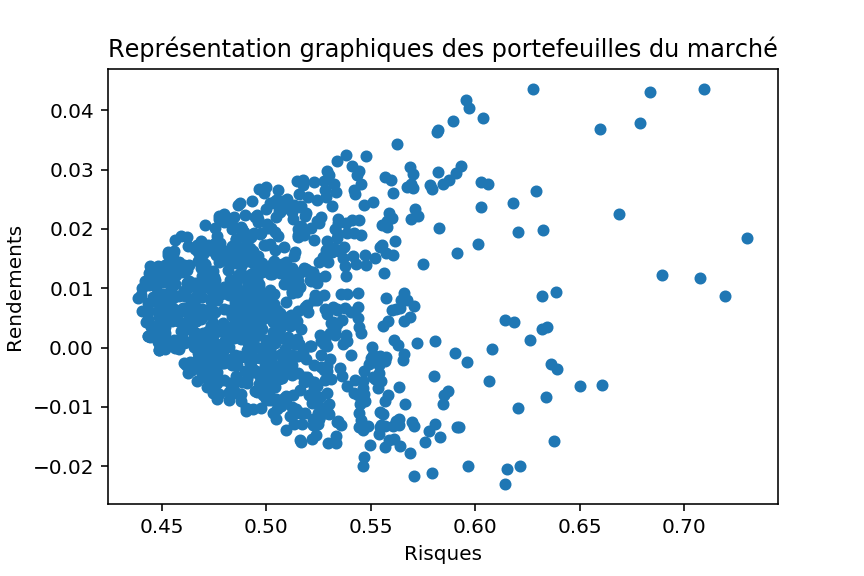
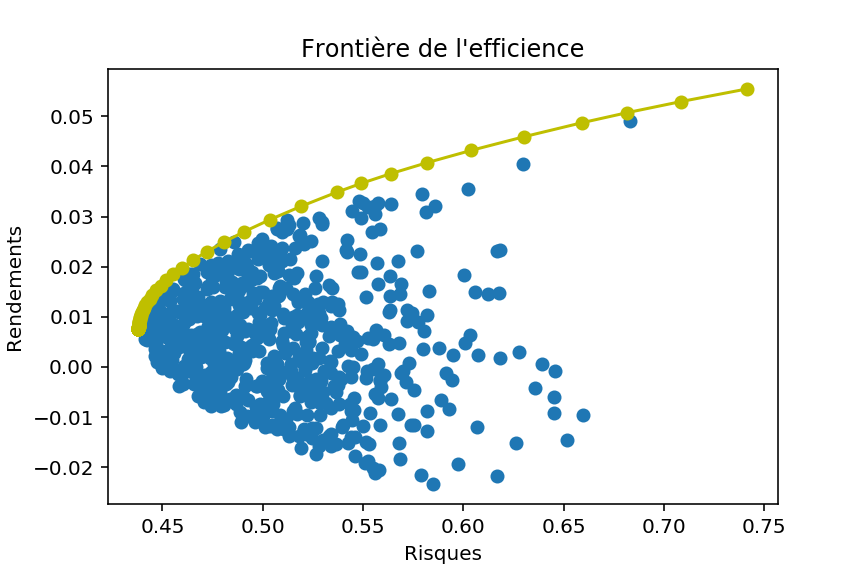
En étudiant le problème des N Corps, il est possible de programmer des simulations informatique sur ce dernier.

En effet, en considérant un ensemble de corps avec chacun, une masse, une position, le tout dans un espace ayant une constante gravitationnelle : les positions successives sont obtenues par l’application de la seconde loi de Newton où chaque corps subit la force des N-1 autres.

Mon programme (simple) en Python permet d’obtenir ceci :

D’autres simulations plus élaborées (et plus gourmandes en ressources!) permettent d’obtenir de bien meilleures simulations, comme par exemple le projet SpaceSim :

Code Python :

Après avoir parlé des automates cellulaires et du jeu de la vie, je n’ai pas résisté à l’envie de tester ça moi-même !

Une compilation des patterns qui m’ont le plus impressionné :

Code Python :

Un portefeuille efficient est un portefeuille d’actifs financiers permettant d’optimiser le couple rendement/risque grâce à une diversification judicieuse.

La théorie du portefeuille efficient a été développée par Harry Markowitz (l’un des Prix Nobel d’économie 1990) dans les années cinquante afin d’offrir la rentabilité maximale pour un niveau de risque défini, qui soit aussi faible que possible.

Sur le plan technique, il s’agit d’un problème d’optimisation quadratique, son originalité est essentiellement l’application de ce modèle mathématique au monde de la finance.

Le modèle de Markowitz, permet donc, à partir d’une série de portefeuilles, de répondre à la question : Comment choisir le meilleur portefeuille, pour un niveau de risque donné ? Autrement dit, comment maximiser mon rendement, pour un niveau de risque ? (Ou encore : comment minimiser mon risque, pour un niveau de rendement souhaité).

Code Python :