Auteur/autrice : LMeg

Publié le

Propagation du Coronavirus en Python

Les différentes décisions prises dans beaucoup de Pays sur le confinement, ou sur d’autres sujets (achats de masques médicaments, etc..) sont basées sur des projections, ces dernières sont obtenues par le biais de simulations, et ces simulations suivent un modèle mathématique, et sont pour la plupart fournies par le prestigieux Imperial College of London.

Cela montre en quoi les mathématiques associées à l’informatique peuvent être un merveilleux outil au service de l’humanité.

Dans le cas d’un virus comme le Covid-19, la croissance est en effet exponentielle au début. Mais il est clair que cela ne peut pas continuer éternellement. À un moment donné, le virus manquera de ressources, c’est-à-dire de personnes susceptibles d’être infectées, car une grande partie de la population l’est déjà ou l’a déjà été. Ensuite, le nombre de cas n’augmente que de façon linéaire, c’est-à-dire de façon constante chaque jour. Et, encore plus tard, la croissance de la courbe s’arrête complètement. C’est exactement ce que décrit l’équation logistique ci-dessus :

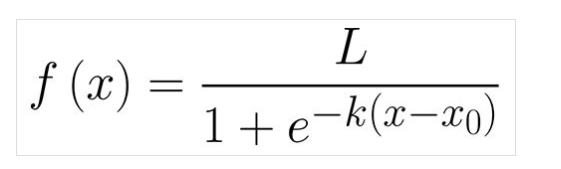
Source : pourlascience – À noter que cette fonction décrit de façon approximative la propagation du virus, c’est la seule que j’ai pu trouver sur internet.

J’ai voulu comprendre le sens mathématique de ces simulations, pour les reproduire moi même en Python, en considérant les paramètres suivants :

  • X indique le temps, supposons qu’il commence au jour 0 et s’arrête après 50 jours.
  • X0 indique le moment où la croissance exponentielle s’arrête, disons après 30 jours.
  • L indique la valeur maximale pouvant être par la courbe (nombre de cas), disons 4.5 10^-4 de la population française, soit 30000
  • K indique la pente de la courbe : disons 0.5
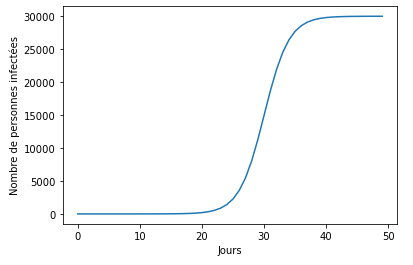
Résultat de la simulation, après le 20ème jour d’apparition du virus, la croissance devient exponentielle avant de se stabiliser au 40ème jour

Ceci est une projection, basée sur une seule simulation, autrement dit, un seul scénario, mais il est tout à fait possible d’en simuler plusieurs, ce qui est fait d’ailleurs par l’Imperial College of London.

Les résultats sont visibles ci-dessous :

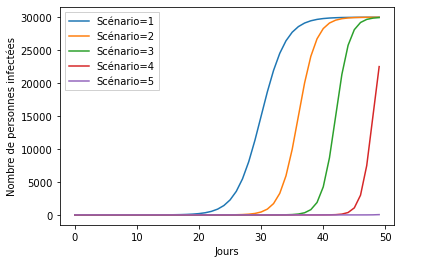
Le détail des scénarios est mentionnés dans le code Python.

Bien sûr, les simulations officielles sont basées sur beaucoup plus de détails et de paramètres, cet article est purement écrit dans un but pédagogique.

Code Python :

Publié le

Le paradoxe des jumeaux et les frères Kelly

Le paradoxe des jumeaux est un paradoxe issu d’une expérience de pensée qui semble montrer que la relativité restreinte d’Einstein est contradictoire. (Mais en réalité non)

Elle se présente comme suit :

Des jumeaux sont nés sur Terre. L’un fait un voyage aller-retour dans l’espace en fusée à une vitesse proche de celle de la lumière, l’autre reste sur terre.

Puisque le temps s’écoule moins vite en fonction de la vitesse alors, pour celui qui est resté sur Terre la durée du voyage est plus grande que pour celui qui est parti dans l’espace, ainsi, le jumeau ayant voyagé rentre plus jeune que son jumeau sur Terre.

Toutefois, celui qui voyage est en droit de considérer, les lois de la physique restant identiques par changement de référentiel, qu’il est immobile et que c’est son frère et la Terre qui s’éloignent à grande vitesse de lui. Il pourrait donc conclure que c’est son frère, resté sur Terre, qui est plus jeune à la fin du voyage. Ainsi chaque jumeau pense, selon les lois de la relativité restreinte, retrouver l’autre plus jeune que lui, c’est là que réside le paradoxe.

La conclusion, admise par l’écrasante majorité des spécialistes, dit que le jumeau voyageur finit plus jeune que celui resté sur Terre, et que cette différence peut être considérée comme due à la dissymétrie entre les jumeaux, car le voyageur change de référentiel galiléen pour revenir, alors que l’autre n’en change pas.

Sur un tout autre sujet, la Station spatiale internationale se trouve à 330-420 km d’altitude de la terre et a une vitesse en orbite de 7,66 km/s.

Et en novembre 2012, la NASA a mené une expérience qui inclut 2 frères jumeaux, tous deux astronautes, Scott Kelly et Mark Kelly.

L’un devra rester sur terre, tandis que l’autre passera une année entière à bord de La Station spatiale internationale, le but de l’expérience étant d’étudier les effets d’une mission de longue durée dans l’espace, sur le corps et le moral humain.

Les frères Kelly en question. À noter que la vitesse de l’ISS (7.66km/s) ne permet pas de réaliser l’expérience des jumeaux, et donc pas de changement concernant leurs âges respectifs.

Pour le jumeau dans l’espace, il a été observé :

6 mois après son retour, les différents éléments sont revenus à la normale, cependant, ça ne serait peut être pas le cas si le voyage avait duré plus d’une année, rien ne peut encore être conclu pour des durées de voyages plus longues.

Publié le

Paradoxe de Russell

Le paradoxe de Russell, est un paradoxe de la théorie des ensembles, il répond à la question suivante :

Existe t-il un ensemble qui contient tout les ensembles ?

Ou formulé autrement, l’ensemble E des ensembles n’appartenant pas à eux-mêmes appartient-il à lui-même ?

  • Si la réponse est oui, E appartient à lui même : comme notre ensemble E contient des ensembles n’appartenant pas à eux-mêmes, on tombe sur une contradiction
  • Si la réponse est non , E n’appartient pas à lui même : comme notre ensemble E contient des ensembles n’appartenant pas à eux-mêmes, il devrait appartenir à lui même, on tombe à nouveau sur une contradiction.

Il y’a donc une contradiction dans les deux cas, ce qui rend paradoxale (et donc impossible) l’existence d’un tel ensemble.

Le paradoxe du barbier est une illustration du paradoxe de Russell, qu’on peut formuler comme suit :

Le barbier du village doit de raser tous les habitants qui ne se rasent pas eux-mêmes et seulement ceux-ci.

  • Si le barbier se rase lui même : alors il ne devrait pas se raser lui même (Car en tant que barbier, il doit raser seulement se rasent pas eux-mêmes)
  • Si le barbier ne se rase pas lui même : alors il remplit la condition de son travail, il doit se raser lui même

On retrouve une contradiction dans les 2 cas.