Le paradoxe de Newcomb est une expérience de pensée faisant intervenir un jeu entre deux joueurs, l’un d’entre eux étant un devin, capable de prédire l’avenir.
Pour l’ingénieur et philosophe français, Jean-Pierre Dupuy ce paradoxe « défie nos intuitions sur la liberté et le déterminisme d’une façon rarement atteinte ailleurs »
Le paradoxe s’énonce comme suit :
- Un joueur joue une partie avec le devin, ce dernier est capable de prévoir les actions du joueur.
- Deux boîtes A et B sont présentées au joueur. Ce dernier a le choix entre prendre le contenu de la boîte A et prendre le contenu des boîtes A et B.
- Au préalable, le devin a rempli les boîtes ainsi :
- La boîte B contient toujours 1 000 € ;
- Le contenu de la boîte A est variable et est déterminé ainsi : si le devin a prédit que le joueur prendrait seulement la boîte A, elle contient 1 000 000 €, mais elle ne contient rien si le devin a prédit que le joueur prendrait les deux boîtes.
Le joueur garde après le jeu le contenu des boîtes qu’il a ouvertes.
Le joueur est au courant de toutes les règles du jeu, y compris des deux contenus possibles de la boîte A, du fait que son contenu est fondé sur la prédiction du devin, et que le devin est infaillible.
Au moment où le jeu commence et où le joueur est appelé à décider de ce qu’il va prendre, la prédiction a déjà été faite, et le contenu de la boîte A est déterminé. En d’autres termes, la boite A contient soit 0 soit 1 000 000 € avant que le match commence, et une fois le jeu commencé, même le devin est impuissant à modifier le contenu des boites.
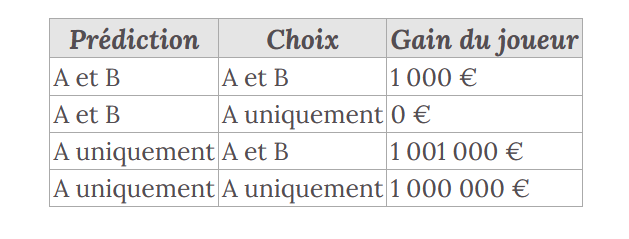
1 – Une première stratégie qui consiste à maximiser son gain consiste à raisonner de la sorte :
Si la prédiction a été que le joueur ne prendra que A, alors prendre les deux boîtes rapporte 1 001 000 €, alors que ne prendre que A ne rapporte que 1 000 000 €.
Si la prédiction a été que le joueur prendra les deux boîtes A et B, alors prendre les deux boîtes rapporte 1 000 €, et prendre juste A rapporte 0€ (Prendre B seule rapporte 1000€ aussi).
Dans tous les cas, décider de prendre les deux boîtes rapporte toujours 1 000 € de plus.
Cette stratégie se fonde sur le fait que la prédiction du devin a été faite hier (au passé), et que par conséquent le contenu des boîtes est déjà fixé : ma décision présente ne pourrait donc pas influencer le contenu des boîtes, qui a été fixé hier. Cette stratégie suppose un libre arbitre.
2 – Une deuxième stratégie consiste à supposer que le devin ne se trompe jamais et qu’il n’y a pas de libre arbitre :
Dans ce cas, prendre seulement la boîte A est un meilleur choix.
Ainsi, selon la stratégie choisie, le choix maximisant le profit est différent.
Un autre aspect paradoxal peut être soulevé : si le devin a pu prédire ce que j’allais faire, c’est que mes actes seraient (en principe) prédéterminés. En même temps, le problème suppose un libre arbitre, sinon le joueur n’a pas réellement la possibilité de faire un choix (le choix étant déjà fait avant que le jeu commence).
La rationalité du choix dépend aussi de ce que l’on pense du devin :
1 – Si on accepte l’affirmation que le devin se trompe rarement, et si l’on accepte que les sommes d’argent ont été effectivement disposées comme indiqué, alors le choix rationnel est celui de la seule boîte A.
2 – En revanche, si l’on nie la possibilité d’une quelconque prédiction (ce qui paraît rationnel), le choix rationnel consiste à ouvrir les deux boîtes.
3 – Mais en même temps, le fait d’agir rationnellement conduit, justement, à avoir un comportement prédictible, ce qui peut finalement justifier la performance du devin : être rationnel, dans ce cas, n’est pas nécessairement rationnel ! Dans ce cas, une façon de briser le pouvoir du devin consisterait à choisir au hasard quelle boite ouvrir. Le devin peut certes savoir quelle boite je vais ouvrir, mais si ce choix est délégué à la parité d’un dé ou à une pièce de monnaie (Pile ou face), le devin pourrait être vaincu car ce n’est plus moi qui décide quelle boite ouvrir.
