Dans une série de nombres, on pourrait s’attendre à voir les chiffres de 1 à 9 apparaître à peu près aussi fréquemment comme premier chiffre de chacun des nombres, soit avec une fréquence de 1/9 = 11,1 % pour chacun.
Contrairement à cette intuition, la série suit très souvent approximativement la loi de Benford, cette loi fait référence à une fréquence de distribution statistique observée empiriquement sur de nombreuses sources de données dans la vraie vie, ainsi qu’en mathématiques.
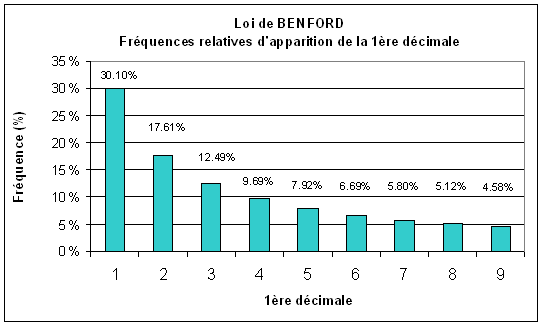
En effet, dans notre série de nombres, pour un tiers des données, le 1er chiffre significatif le plus fréquent est le 1. Viennent ensuite le chiffre 2, puis le 3, etc.
Cette loi est observée aussi bien dans les sciences humaines et sociales, en physique, en volcanologie, génétique, en BTP, en économie ..
Pour tout c entre 1 et 9 (c étant le premier chiffre), la loi s’exprime comme suit : log(1 + 1/c).
Aujourd’hui, on utilise par exemple la loi de Benford pour détecter les fraudes fiscales : si quelqu’un invente des chiffres pour cacher ses revenues, ces derniers ne suivront probablement pas la loi de Benford.
