Une loi empirique est une loi ou une formule issue de faits expérimentaux, ou validée par l’expérience, mais dont on ne connaît pas de base théorique, ou qu’on ne peut pas relier à une base théorique simple.
Ainsi, le second postulat de la première loi de Moore stipule que « le nombre de transistors des microprocesseurs sur une puce de silicium double tous les deux ans. » et se révéla particulièrement exacte entre 1971 et 2001.
En conséquence, les machines électroniques sont devenues de plus en plus petites et de moins en moins coûteuses tout en devenant de plus en plus rapides et puissantes.
En parallèle avec la loi de Moore, la loi (empirique) de Koomey décrit une tendance à long terme dans l’histoire des ordinateurs.
Elle peut être énoncée comme suit : la quantité d’énergie dont une machine a besoin pour effectuer un nombre donné de calculs va diminuer d’un facteur deux chaque année et demie.
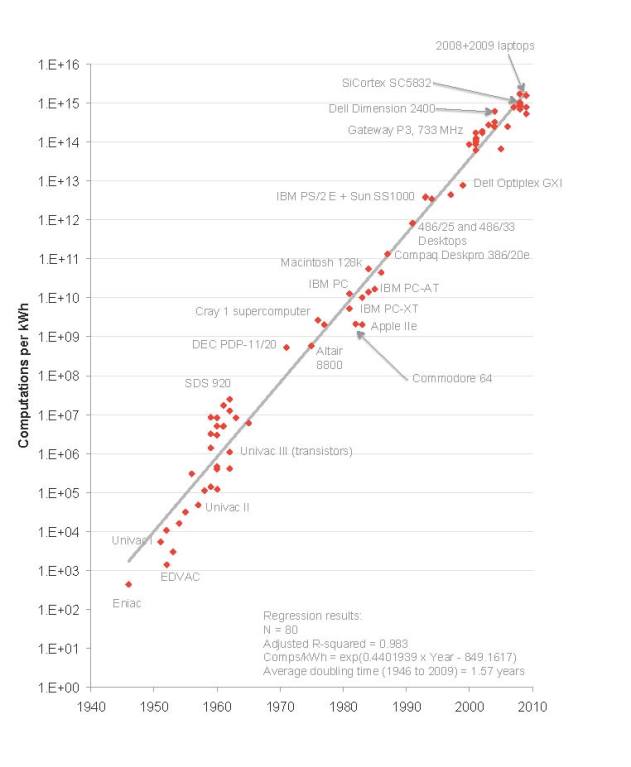
La courbe est le tracé représentant la loi de Koomey, en rouge, le nombre de calculs effectifs (d’où la régression linéaire).
- Avec un raisonnement simple et en suivant cette loi, on peut imaginer qu’en fixant une quantité d’énergie (disons 1 joule), le nombre de calculs qu’une machine peut effectuer, va augmenter chaque année et demie.
- Plus le temps passe, plus ce nombre de calculs croît (ici de manière exponentielle) et sans limites finie.
D’un autre côté, le théorème de Margolus-Levitin, impose une limite fondamentale au calcul.
Selon ce théorème, la vitesse à laquelle toute machine calcule (c’est-à-dire nombre d’opérations effectuées dans un temps donné et utilisant une quantité d’énergie donnée) ne peut pas être supérieur à 6 × 10^33 opérations par seconde et par joule.
Dit autrement, en utilisant un joule il serait possible à une machine de réaliser jusqu’à 6 000 000 000 000 000 000 000 000 000 000 000 (6 millions de milliards de milliards de milliards) d’opérations par seconde, mais sans pouvoir franchir cette limite.
Cette limite est surtout « physique », elle a été calculée par Norman Margolus et Lev B. Levitin, en effet, calculer revient à modifier l’état physique d’un bit d’information. Cette modification a un coût qui peut être borné, ce qui aboutit à la limite mentionnée plus haut.
De quoi bien faire attention aux abus de langages entre une loi empirique et une loi physique !
