L’entropie de Shannon, est une fonction mathématique qui, intuitivement, correspond à la quantité d’information contenue ou délivrée par une source d’information (un texte, un signal électrique, un fichier informatique, une image, …).
L’entropie peut simplement être vue comme l’incertitude qui résulte des messages émis par la source, une source émettant toujours le signal ‘1’ aura une entropie nulle (pas d’incertitudes quant aux messages suivants), si le signal alterne entre ‘1’ et ’11’, l’entropie est > 0.
En d’autres termes, l’entropie de Shannon représente quantitativement l’incertitude qui règne sur l’information émanant de la source, elle indique alors la quantité d’information nécessaire pour que le récepteur puisse déterminer sans ambiguïté ce que la source a transmis. Plus le récepteur reçoit d’information sur le message transmis, plus l’entropie (incertitude) vis-à-vis de ce message croît.
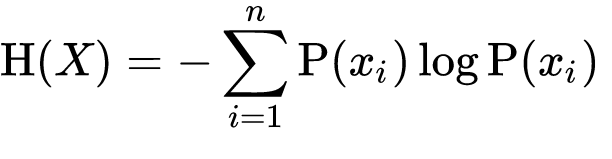
L’entropie de X (H(x)) est formellement définie suivant la formule.
L’entropie de Shannon est utilisée en imagerie (médicale ou spatiale) elle permet notamment de recaler deux images différentes l’une sur l’autre en minimisant l’entropie des deux images.
En pratique cela permet de comparer les scanners d’un patient A quelconque avec un patient de référence B. Enfin, en génétique, l’entropie de Shannon permet de repérer sur un chromosome les portions d’ADN contenant le plus d’information.
