En informatique théorique, une machine de Turing est un modèle abstrait (un modèle mathématique) du fonctionnement des appareils mécaniques de calcul, tels un ordinateur, une calculatrice, etc…
Ce modèle a été imaginé par Alan Turing en 1936, en vue de donner une définition précise au concept d’algorithme ou de « procédure mécanique ».
Une machine de Turing comporte les éléments suivants :
- Un ruban infini divisé en cases consécutives. Chaque case contient un symbole d’un alphabet fini donné. L’alphabet contient un symbole spécial appelé « symbole blanc » et un ou plusieurs autres symboles. Le ruban est supposé être de longueur infinie vers la gauche ou vers la droite, en d’autres termes la machine doit toujours avoir assez de longueurs de ruban pour son exécution. On considère que les cases du ruban contiennent par défaut le « symbole blanc » ;
- Une tête de lecture/écriture qui peut lire et écrire les symboles sur le ruban, et se déplacer vers la gauche ou vers la droite du ruban ;
- Un registre d’état qui mémorise l’état courant de la machine de Turing. Le nombre d’états possibles est toujours fini, et il existe un état spécial appelé « état de départ » qui est l’état initial de la machine avant son exécution ;
- Une table de transitions qui indique à la machine quel symbole écrire sur le ruban, comment déplacer la tête de lecture et quel est le nouvel état, en fonction du symbole lu sur le ruban et de l’état courant de la machine.
Les machines de Turing permettent d’effectuer des calculs, et d’autres opérations, par exemple la machine suivante permet de construire la suite 01010101010101 à l’infini :
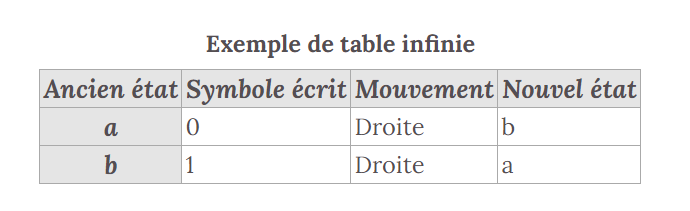
On peut imaginer d’autres usages plus «utiles» comme la réalisation d’opérations mathématiques complexes.
