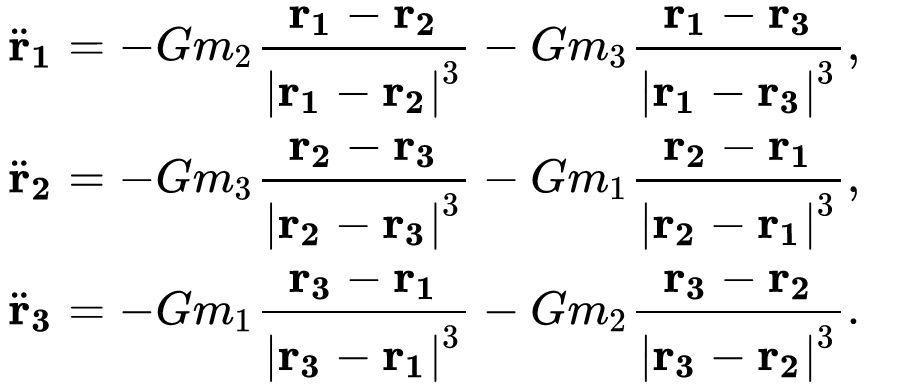Samuel Brannan, (1819 – 1889) est un homme d’affaires américain qui fit fortune grâce à la ruée vers l’or en Californie, au milieu du XIXe siècle.
Comment ce dernier a fait fortune ? Ces quelques dates clés retracent son histoire :
- En 1848, il se rend à Sutter’s Mill, près de Coloma où de l’or avait été découvert.
- Dans la même année, il a d’abord prétendu et propagé la nouvelle que c’était faux, aucun or n’avait été découvert : il avait fait cela durant 2 mois, le temps de vérifier et de préparer ses commerces.
- Il prit soin d’acheter tout le matériel de chercheur d’or disponible à des kilomètres à la ronde, ceci dans le but d’en devenir l’unique fournisseur.
Quelques mois plus tard, Brannan devint l’homme le plus puissant de l’Ouest Américain, son magasin lui rapportant 2 000 000 de dollars actuels par mois. Il ouvrit plusieurs magasins pour vendre du matériel aux mineurs et acheta plusieurs terrains à San Francisco dès lors qu’il apprit l’arrivée des grands groupes miniers de l’Est attirés par la ruée vers l’or.
Cette puissance financière s’accompagna par d’autres projets : commerce international, banques et compagnies de chemin de fer, mais aussi d’une puissance politique, où il fut élu au Sénat de Californie en 1853.
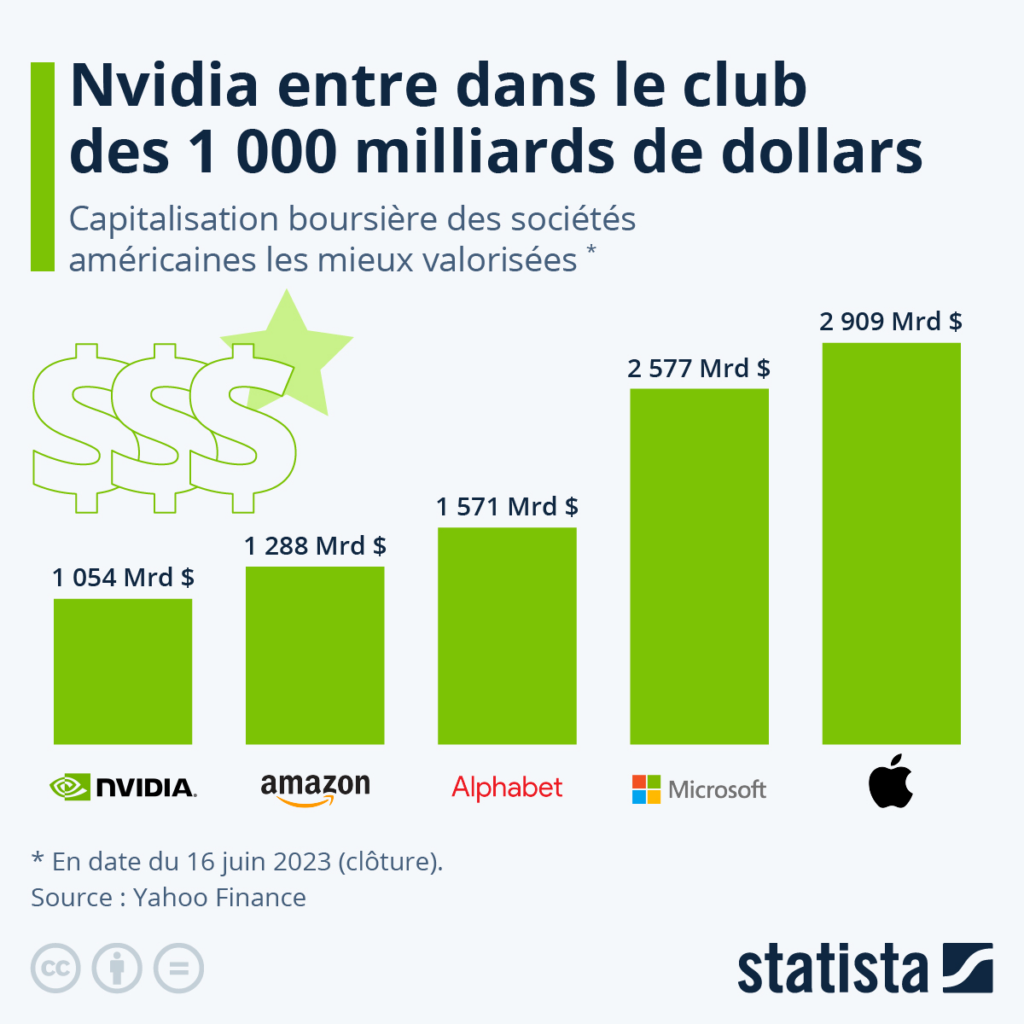
De nos jours, un parallèle est fait avec l’émergence de l’intelligence artificielle, comme l’attestent de récents articles de presse : «L’intelligence artificielle : une nouvelle ruée vers l’or ?».
En effet, dans ce contexte, certains estiment que les vrais vainqueurs de l’émergence de l’intelligence artificielle sont les constructeurs de GPU (cartes graphiques) plutôt que les utilisateurs et adeptes de l’IA, comme le fut à l’époque Samuel Brannan vendeur de matériel pour miner de l’or, plutôt que les mineurs d’or eux mêmes.
Après son divorce et à cause de sa dépendance à l’alcool, il finit ruiné et mourut à l’âge de 70 ans, à méditer !