En mathématiques, une closed-form expression, est une expression mathématique utilisant un nombre fini d’opérations standards (+ − × ÷, variables, constantes..), par exemple 4 = x + 2.
Contrairement à l’équation précédente dont la solution est x = 2 (un entier numérique), une équation différentielle est une équation dont la ou les inconnues sont des fonctions;
Certaines (un prochain article expliquera pourquoi) équations différentielles n’ont tout simplement pas de solutions finies sous forme « closed-form expression ».
Ainsi, Le problème à N corps est un problème de mécanique céleste consistant à déterminer les trajectoires d’un ensemble de N corps s’attirant mutuellement : il s’agit de résoudre les équations du mouvement de Newton pour N corps interagissant gravitationnellement, connaissant leurs masses ainsi que leurs positions et vitesses initiales : c’est la seconde loi de Newton.
Le cas N = 2 (problème à deux corps) a été résolu par Newton, mais dès N = 3 (problème à trois corps) apparaissent des solutions essentiellement impossibles à expliciter, car on se retrouve dans un système chaotique (sensibles aux conditions initiales).
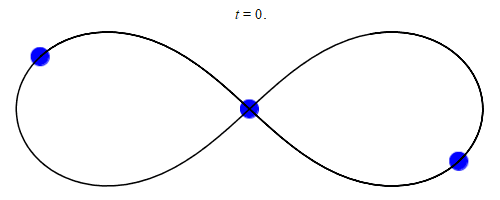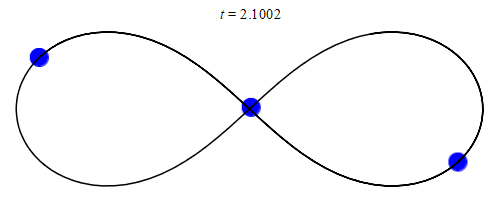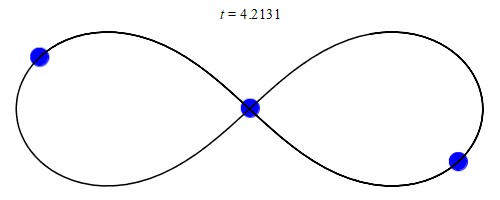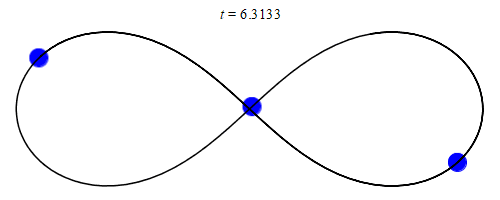
En effet, dans un système à 2 corps, il y a un barycentre statique. Cela simplifie énormément la situation, car le vecteur de force sur les deux corps pointe toujours vers le barycentre. Si le barycentre ne bouge pas, alors les deux corps sont en orbite autour d’un point fixe (même si ce point n’est pas à l’intérieur de l’un ou l’autre des corps).
Dans un système à trois corps, cependant, le barycentre se déplace à mesure que le système évolue; par conséquent, le vecteur de force agissant sur chaque corps (et donc le vecteur d’accélération de chaque corps) se déplace constamment. Cela rend un système à trois corps chaotique. (Un système chaotique est toujours déterministe – c’est-à-dire que l’état futur de chaque corps est toujours déterminé par les positions et les vitesses des corps à l’heure actuelle – mais il ne peut pas être décrit ou prédit par une équation finie).
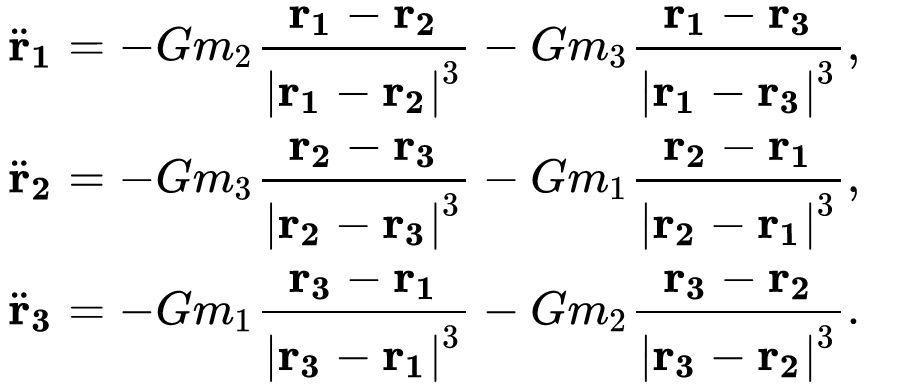
En utilisant un ensemble d’approximations (et de superordinateurs), nous pouvons prédire les positions des corps dans un système à N corps (comme notre système solaire ou une galaxie qui sont des problèmes à N corps) avec une assez bonne précision. Même ceci est différent que de résoudre le problème à N corps !
Indépendamment de notre capacité à prédire où la planète Naboo se trouvera le 06 Novembre 2074, nous n’avons pas décrit (et ne pouvons pas décrire) la position de Naboo avec une simple équation finie. C’est cela le problème des N-corps.
