Le problème de Monty Hall est un casse-tête probabiliste librement inspiré du jeu télévisé américain Let’s Make a Deal.
Il porte le nom de celui qui a présenté ce jeu aux États-Unis pendant treize ans, Monty Hall.
Le jeu oppose un présentateur à un candidat (le joueur). Ce joueur est placé devant trois portes fermées. Derrière l’une d’elles se trouve une voiture et derrière chacune des deux autres se trouve une chèvre. Il doit tout d’abord désigner une porte. Puis le présentateur doit ouvrir une porte qui n’est ni celle choisie par le candidat, ni celle cachant la voiture (le présentateur sait quelle est la bonne porte dès le début). Le candidat a alors le droit d’ouvrir la porte qu’il a choisie initialement, ou d’ouvrir la troisième porte.
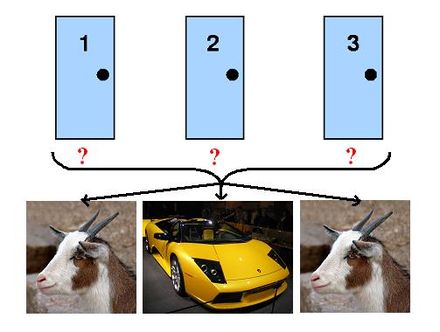
Les questions qui se posent au candidat sont :
- Que doit-il faire ?
- Quelles sont ses chances de gagner la voiture ?
Les stratégies :
Initialement, le joueur peut choisir entre deux stratégies :
- Changer de porte
- Ne pas changer de porte
Au début, on pourrait penser qu’en changeant de porte, on se ramène au jeu initiale mais avec uniquement 2 choix (donc 2 portes) ce qui fait une probabilité de 1/2 de gagner, peu importe le choix.
Cette réflexion est consultable ici.
Néanmoins, on peut démontrer mathématiquement, et de plusieurs manières, que le joueur en changeant de porte, augmente et voit ses chances de gagner passer de 1/3 à 2/3
Aussi contre-intuitif que cela puisse paraître, c’est bien vrai, et on peut s’en convaincre de façon informatique, en simulant des milliers de parties jouées !
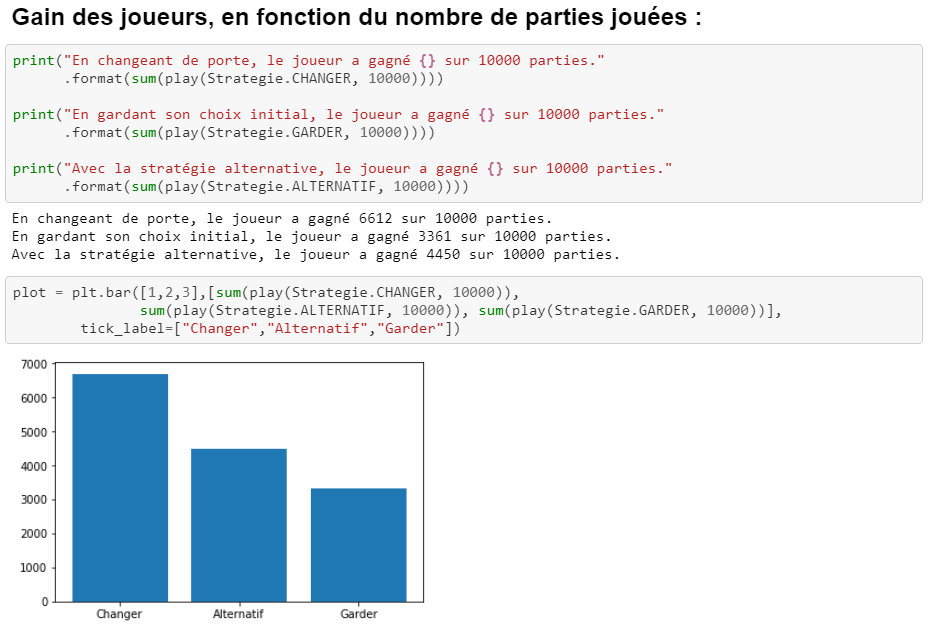
Le code source peut être consulté dans son intégralité sur mon compte GitHub
La démonstration mathématique est rigoureusement bien faite sur Wikipédia
